Followup on Newtonian mechanics in KSP

After I posted my article on implementing Newtonian trajectories in KSP last September, I started a thread in the game's official forums to discuss it and had some interesting conversations over the next few weeks.  Ever since then I've been meaning to post a followup article to bring together some of the points from those conversations, but until now haven't managed to actually write anything.  But finally, about five months later, I've gotten around to it!  Here goes:

TL;DR

I was not surprised that most commenters in the thread didn't read my original article.  When I wrote it I didn't want to just explain my scheme for implementing Newtonian mechanics in KSP, I wanted to make it possible for someone who did not know anything about numerical methods to understand why I defined my scheme the way I did and why certain methods would or would not work.  I was more interested in educating than advocating.  That inevitably made the article very long, and in the end probably very few would be interested in reading it all the way through.

But I was surprised at how many people seemed to read only the title of the forum thread ("On Newtonian trajectories vs. patched conics") before writing a reply to give their views on the subject, without reading the conversation in the thread or even the first post!  I'm not going to dwell on it further; I suppose it is just human nature as applied to Internet forums.  But it did strike me rather strongly at the time and I wanted to note it.

Recap

In the spirit of TL;DR I think I should start by summarizing the first article and some brief points that came out of the forum thread:

• Here I am looking at what can be called a restricted N-body problem.  The goal is to have vessels and debris in space follow Newtonian trajectories, subject to the gravity of the bodies in the KSP solar system (sun, planets, and moons).  The planetary bodies themselves stay on their Kepler orbits, and the vessels don't feel any gravitational attraction between themselves.  Thus the trajectory of each vessel is calculated independently of all the others.
• Each vessel is treated as a point mass for the purposes of calculating its trajectory.  The trajectory of each part is not calculated independently.  Thus this has no impact on the part-to-part physics calculations that seem to become the performance bottleneck for most players.
• My proposed scheme is a hybrid, in which Kepler orbits would still be used at sufficiently low altitudes around each body.  Thus each body would still have a SOI in which things still operate as they do now in the game, it would just be much smaller than currently.  Newtonian trajectories would be used only in the 'no-man's land' outside of those SOIs.  For example, for Kerbin I would use an SOI radius somewhere between about 4 to 6 Mm.
• As a result of the hybrid scheme, vessels in low orbits that the player expects to be stable would still be stable.  For the example of Kerbin the reduced SOI would still encompass orbits up to and including synchronous orbits.  So the player's space station in low orbit and communication satellites in synchronous orbits would not be in any danger of drifting away or crashing into the planet.  Orbits that are partially or fully in 'no-man's land' should be assumed to be unstable.
• The transition point between Kepler and Newtonian trajectories would be visible to the player, just as SOI transitions are now.  There should never be a reason for the player to be surprised by a vessel having an unstable orbit.
• The other advantage of the hybrid scheme is that it reduces computational effort.  Low orbits require the smallest time steps to integrate, and in most games most vessels and debris will be in low orbits around Kerbin or other bodies.
• It is absolutely possible to numerically integrate the trajectory of a vessel with high accuracy without too much of a computational load, but using a numerical scheme with reasonably high order of accuracy is vital.  If you think numerical integration of trajectories couldn't work because you've tried it before using Euler or Velocity Verlet integration, well, those schemes are not the last word in numerical integration.  I found that a fifth-order Runge Kutta scheme is about one hundred times faster than VV and should be good enough.
• It is important to use a numerical scheme with an adaptive time step, because there is no way of knowing ahead of time what kind of trajectory the player will put his or her vessels on.  A vessel in high Kerbin orbit needs a time step of about 100 s, while a vessel in solar orbit out around Eeloo can use time steps of about 10 Ms. Specifying an error limit for an adaptive scheme rather than a fixed time step means there is no risk of having orbits go haywire under high timewarp.  Instead, if there are too many trajectories to calculate timewarp will have to slow down.
• Trajectories would normally be precalculated for vessels and debris, so that they can be shown in map view.  If the player enters timewarp without disturbing the vessel's trajectory, it will follow that precalculated trajectory on a rail.  The player would still be able to see where his/her vessel is going ahead of time in map view.  The distance that a trajectory can be precalculated while a vessel is maneuvering depends on the player's computer.
• Interpolation functions can be calculated for every step of the precalculated trajectory, to allow a vessel's location to be calculated at any arbitrary time.  (The player would not see vessels jumping from one point to another every 100+ seconds, as the long timesteps used for integration pass.)

Now, on to a few points that deserve a little more detail.

Speed revisited

The concern that comes up again and again is that numerically integrating a trajectory is so hard it would make your computer melt or, less dramatically, it is too slow to handle the 100,000x timewarp that we are accustomed to.  But it's just not true!  I discussed computational speed briefly in my first article, but I did some followup tests that are worth mentioning here.

My original code, which I tried to write to be efficient, could calculate around 10k - 12k time steps per second on my laptop.  My laptop has a 1.73 GHz Core i7 processor, and the key figure there is the processor speed, 1.73 GHz.  My program is single-threaded, so it doesn't matter how many cores my CPU has or whether it has hyperthreading.  The program also doesn't use any SIMD instructions, at least as far as I'm aware.

I originally said that I wasn't especially interested in exploring code optimizations.  But I got curious and decided to see what the bottlenecks were and how tough it would be to make the code run faster.  Most of the original program's time was spent in the routine that calculates each body's position from its Kepler orbit elements.  I thought that the slowdown was glibc's implementation of sine and cosine, but it turns out the compiler was already optimizing them to CPU instructions.  I was able to get the speed up to about 20k steps per second by cleaning up the position-from-Kepler-elements routine, but eventually the main bottleneck was the sine and cosine instructions.  I discovered a new compiler optimizer setting (-ffast-math) that caused the compiler to replace separate sine and cosine instructions with one x87 fsincos instruction, and that brought the speed up to around 30k steps per second.  But that was the best I could do with Kepler orbit elements.

I had seen discussions on the internet about approximating sine and cosine using functions that sacrifice some accuracy to obtain better speed.  This sounded like an interesting route to try, but as long as I was sacrificing accuracy I thought it made more sense to approximate each body's position directly.  So, I wrote a routine that divided a body's orbit into equal steps and calculated a fifth-order interpolating function for the position of the body within each step.  I played with the number of steps for each body to find the minimum number of steps needed to keep the maximum position error for the body under 1 m.  This number turned out to be between eleven (Ike) and 118 (Eeloo), and the total amount of data that had to be stored for all bodies' orbits was about 100 kB.  When I ran simulations using those interpolating functions I got up to about 60k - 75k steps per second (depending on the load on the other CPU cores), and the accuracy of the simulated trajectory wasn't decreased very much.

Given that a program can run full-out on ore core and calculate 60k+ steps per second, I think my initial estimate that at least 50k steps per second could be calculated in the game is plausible.  (In the game, there would be additional overhead of calculating multiple trajectories at once, checking for SOI transitions, etc.)  So, what does 50k steps per second mean?  Well, with the SOI radius for Kerbin I've specified, a vessel in circular orbit just above the SOI limit would need time steps of about 100 s to calculate its trajectory.  I'll make the blind assumption that a similar SOI can be defined for each other body so that time steps shorter than 100 s, on average, are never needed.  If I can calculate 50k steps per second, and each step is 100 s long, then I can calculate 5 Ms worth of trajectory per second.  That means I can calculate the trajectory of 50 vessels (or pieces of debris) at 100,000x time warp.  In this worst-case scenario, if I have more than 50 vessels the 100,000x timewarp would have to start running slower.  But, this is a worst-case scenario!  It is highly unlikely that a game would have many vessels in orbit just above the SOI boundary; in practice most vessels or debris outside any body's SOI would be on an interplanetary trajectory, and in interplanetary space time steps can be millions of seconds long.  In that case we could expect to be able to calculate hundreds or thousands of trajectories at 100,000x timewarp.  All this assumes, of course, that the routine calculating these trajectories is running in its own thread, so that it can run 100% of the time on its own core.  If the numerical integration scheme has to run in the same thread as the rest of the game, the slowdown would start happening sooner.  This is also based on the performance of my not-all-that-fast laptop; the clock speed of my newer desktop is about twice as fast, and the program accordingly runs about twice as fast.

Long-term behavior revisited

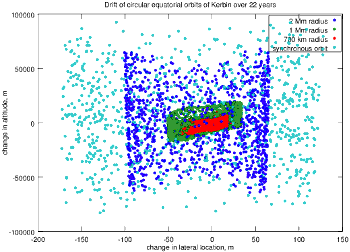Many posters expressed concern (or their belief that) numerically integrating the trajectories of vessels would make players' space stations, satellites, etc. fall out of the sky when they aren't looking.  The hybrid scheme I described addresses this completely (see TL;DR above), but never mind that.  In my original article I looked at long-term behavior of some orbits, but I only looked at a year's worth of behavior and I only considered equatorial orbits.  We can do better than that, and I've been curious to try.  The longest-lasting mission I've ever seen is allmhuram's epic journey that he made using only the parts available at the beginning of career mode, which lasted about 22 years.  I think it's safe to take that length of time (700 Ms, or about 22.2 years) as the longest that any player is likely to ever have their attention directed away from Kerbin.

I first revisited equatorial circular orbits, looking at a low orbit (100 km altitude, or 700 km orbit radius), two medium orbits (1 Mm and 2 Mm radii, or 300 and 1300 km altitude), and a Kerbin-synchronous orbit (about 2.87 Mm radius).  The figure at left shows how these orbits behave over 22 years.  The lateral (north-south) drift is small in every case, covering only about 60 m for the lowest orbit and about 300 m for the highest one.  The variation in altitude is larger -- about ±10 km for the lowest orbit, which might be a bit scary to see when the orbit is only 30 km above the edge of the atmosphere to begin with, but it shows no sign of imminent decay into the atmosphere.  Variation for the synchronous orbit is ±100 km, which does not bode well for the satellite actually remaining Kerbin-synchronous, but again the satellite is in no danger of hitting the planet or of being ejected from orbit.  All of this is very similar to what I originally saw when looking at one year's worth of behavior; it just shows that the fairly stable behavior continues for a longer time.

I should pause here and explain just what data is plotted in the figure.  At the beginning of each simulation, I define a plane that goes through the vessel's initial position and is perpendicular to the vessel's initial velocity.  This plane stays fixed relative to Kerbin.  For the rest of the simulation, every time the vessel crosses the plane going in its original direction, I interpolate its path to find its exact location as it crosses the plane and I record the coordinates.  I use that data to make these plots.  I can't plot the actual orbits; over 22 years the vessel makes hundreds of thousands of orbits!  Plotting that would require tens of millions of data points and the plotting code in Octave would just curl up and die, and even if the plot could be made it would just look like a solid blob.  The first plot also shows points for only about 1 in 200 orbits to avoid overloading the plot.  These plots based on where the orbit crosses a fixed plane can't show the shape of the orbits, but they do give an idea of how much it is shifting around.

NOW, the equatorial orbit is a special case because it is in the same plane as Kerbin's orbit, Mun's orbit, and the orbits of most other bodies in the system.  There is hardly any perturbation out of the plane of the orbit; the slight lateral drift that does show up is probably due to Minmus.  So I did another set of simulations using the same orbital radii but with the orbital inclination set at 45 degrees.  The figure at right shows how different the long-term behavior is in this case.  Recalling that the plot only shows where the orbit crosses a fixed plane, we can interpret the large sweeps north and south as precession of the orbit over time, which in itself would probably not be that much of a concern for most players.  But the orbits clearly change in altitude quite a bit, and in fact the two lower starting orbits (1 Mm and 700 km radii) do end up falling into Kerbin after several years!  This result was quite surprising to me; my initial focus on equatorial orbits blinded me to this behavior until I thought to check inclined orbits now, months after writing and discussing the original article.  This result means the hybrid scheme that retains Kepler orbits at low altitude is more important than I realized.

L-points revisited

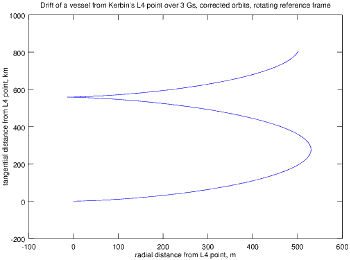The forum thread got sidetracked for a while by Lagrangian points.  A few posters commented to the effect that this scheme is a very overcomplicated way to go about introducing L-points to the game, and they could be 'faked in' much more easily.  It is absolutely true that something approximating an L-point could be added to the game fairly easily.  In fact, the way the game is written now you can put a vessel where an L4 or L5 point ought to be and, if you can adjust its velocity precisely enough, you can get it to stay in the vicinity for a long time.  Of course, the point of this scheme isn't L-points.  Indeed, some tests I ran at the time suggested that L-points wouldn't even exist in my proposed scheme.  It is logical that they wouldn't exist: taking the Kerbin - Kerbol system's L4 point as an example, the problem is that the L-point relies on a precise balance of gravitational forces from both bodies.  Looking at forces parallel to the vessel's motion, at the L4 point the vessel is pulled 'backwards' against its motion by Kerbin, which is balanced by Kerbol pulling the vessel slightly 'forward'.  That works because Kerbin, Kerbol, and the vessel all mutually orbit their center of mass.  Because Kerbol is offset a bit from that center of mass, it is able to pull 'forwards' exactly the right amount to balance Kerbin's pull 'back'.  Well, in KSP this condition doesn't hold -- Kerbol is in fact perfectly stationary, and the orbits of all the planets are centered at Kerbol's center.  That difference upsets the delicate balance of forces that creates the L-points.

My original article showed how a vessel placed at Kerbin's L4 point would spiral away from it over the course of about a year and a half, ending up about 65 Mm away from its starting position.  To check that this drift wasn't just due to a programming error, I modified the code to make Kerbin and Kerbol both orbit their center of mass and then tried the simulation again.  The result is shown at left.  The vessel still drifts away from the L-point, but after 3 Gs (about 95 years) it has only gone 800 km!  That residual drift is probably due to my not typing in enough significant digits when entering the Kepler orbital parameters of Kerbol's orbit; the path of Kerbol around the barycanter is only accurate to about five significant figures.  The figure on the left is shown in a rotating reference frame; otherwise the figure would show a very dense spiral and it would be difficult to discern anything from it.  I ran this simulation for a much longer time because one poster in the forum thread asked for it after I posted a similar figure there showing only 50 Ms worth of drift.  The question whether this was drift away from the L-point or if the vessel would follow something like a halo orbit over a longer time period.  This shows that, in the long term, the vessel just drifts away from the L-point.  I think this also shows pretty clearly that the L4 and L5 points can not exist where they are supposed to as long as the solar system is set up the way it is in KSP.

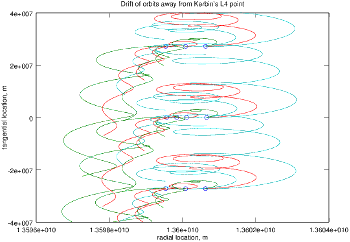
But, what if there is something like an L-point, just not exactly where it would be expected?  I ran a number of simulations in which the vessel's starting position and velocity were adjusted slightly from Kerbin's expected L4 location, to see if I could find something like a Lagrangian point.  An example of these simulations is shown at right.  The figure is also shown in a rotating reference frame to make things slightly easier to interpret.  The x-axis is distance from Kerbol, and y-axis is distance from the expected L4 point location in the tangential direction.  Kerbin is located upwards.  The blue circles show starting points, and the green, red, and cyan curves show trajectories starting with slower than normal, normal, and faster than normal starting velocities respectively.  The figure is a bit of a mess to look at, but the takeaway is that there isn't anything like a stable point anywhere in the vicinity.  In all cases, the tendency is to slow down (due to the pull of Kerbin), then descend into a lower orbit and pull further ahead of Kerbin.  It's possible that there is a stable L4-like point that I just haven't found, but I don't think it exists in this scheme.

Closing

I'll stop now to keep this article to a more reasonable length.  One poster in the forum talked about trying to visualize the equivalent of the interplanetary transport network in the KSP solar system.  I still think that would be a cool thing to do, but haven't even started to think about how to do so.  There was brief discussion of implementing this hybrid Newtonian mechanics scheme in a mod for KSP, but it never went anywhere.  That is still something I would like to try doing, but the learning curve of figuring out Unity, C#, and whatever amount of KSP's internals are exposed to modders dissuaded me.  Since I haven't tried it, I can't say whether it is even possible to do in a mod; whether there is enough of the game made available to the modder to make such a change to the game's engine.  I hope it is!  Finally, a while later I got curious about how the KSP solar system itself would behave under Newtonian mechanics, and I eventually did some simulations of that and posted animations of the results on YouTube.  I'll write a separate article to discuss those, though.